【2428】Maximum Sum of an Hourglass Medium

You are given an m x n integer matrix grid.

We define an hourglass as a part of the matrix with the following form:

Return the maximum sum of the elements of an hourglass.

Note that an hourglass cannot be rotated and must be entirely contained within the matrix.

Example 1:

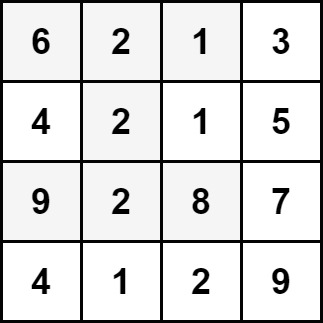
Input: grid = [[6,2,1,3],[4,2,1,5],[9,2,8,7],[4,1,2,9]]
Output: 30
Explanation: The cells shown above represent the hourglass with the maximum sum: 6 + 2 + 1 + 2 + 9 + 2 + 8 = 30.

Example 2:

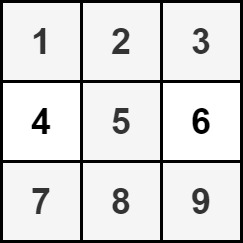
Input: grid = [[1,2,3],[4,5,6],[7,8,9]]
Output: 35
Explanation: There is only one hourglass in the matrix, with the sum: 1 + 2 + 3 + 5 + 7 + 8 + 9 = 35.

Constraints:

• m == grid.length
• n == grid[i].length
• 3 <= m, n <= 150
• 0 <= grid[i][j] <= 106

💡Solution

very easy question but a little bit tricky.

 1public int maxSum(int[][] grid) {
 2    int row = grid.length;
 3    int col = grid[0].length;
 4    int sum = 0;
 5    for(int i =0;i< row -2 ;i++){
 6        for(int j =0;j< col - 2 ;j++){
 7            int count = 0;
 8            count = grid[i][j] + grid[i][j + 1] + grid[i][j + 2] + grid[i + 1][j + 1]
 9                    + grid[i + 2][j] + grid[i + 2][j + 1] + grid[i + 2][j + 2];
10            sum = Math.max(sum,count);
11        }
12    }
13    return sum;
14}

🔗 Refer links

https://leetcode.com/problems/maximum-sum-of-an-hourglass/description/